Reading Time: 4 minutes

Hypothesis Testing of proportion-based samples

Part 2 of our Introduction to Hypothesis Testing series.
by Daniel Bray, posted 20/03/2020

In part one of this series, I introduced the concept of hypothesis testing, and described the different elements that go into using the various tests. It ended with a cheat-sheet to help you choose which test to use based on the kind of data you’re testing.

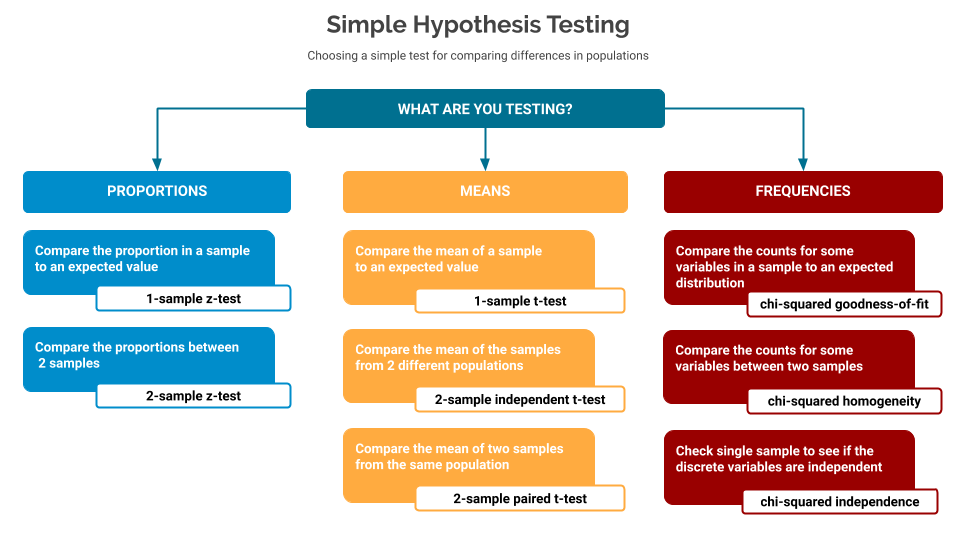
In this second post I will go into more detail on proportion-based samples.

If any of the terms Null Hypothesis, Alternative Hypothesis, p-value are new to you, I’d suggest reviewing the first part of this series before moving on.

What is a proportion-based sample?

In these cases we’re interested in checking proportions. For example 17% of a sample matches some profile, and the rest does not. This could be a test comparing a single sample against some expected value, or comparing two different samples.

Note: These tests are only valid when there are only two possible options; and if the probability of one option is p, then the probability of the other must be (1 – p).

Requirements for the quality of the sample

For these tests the following sampling rules are required:

Random

The sample must be a random sample from the entire population

Normal

The sample must reflect the distribution of the underlying population. For these tests a good rule of thumb is that:

Given a sample size of n
Given a sample proportion of p
Then both np and n(1-p) must be at least 10

For example: if a sample finds that 80% of issues were resolved in 5 days, and 20% were not, then that sample must have at least 10 issues resolved within 5 days, and at least 10 issues resolved in more than 5 days.

Independent

The sample must be independent – for these tests, a good rule of thumb is that the sample size is less than 10% of the total population.

Code Samples for Proportion-based Tests

Note that all of these code samples are available on Github. They use the popular statsmodels library to perform the tests.

1-sample z-test

Compare the proportion in a sample to an expected value

Here we have a sample and we want to see if some proportion of that sample is greater than/less than/different to some expected test value.

In this example:

We expect more than 80% of the tests to pass, so our null hypothesis is: 80% of the tests pass
Our alternative hypothesis is: more than 80% of the tests pass
We sampled 500 tests, and found 410 passed
We use a 1-sample z-test to check if the sample allows us to accept or reject the null hypothesis

To calculate the p-value in Python:

from statsmodels.stats.proportion import proportions_ztest

# can we assume anything from our sample
significance = 0.05

# our sample - 82% are good
sample_success = 410
sample_size = 500

# our Ho is  80%
null_hypothesis = 0.80

# check our sample against Ho for Ha > Ho
# for Ha < Ho use alternative='smaller'
# for Ha != Ho use alternative='two-sided'
stat, p_value = proportions_ztest(count=sample_success, nobs=sample_size, value=null_hypothesis, alternative='larger')

# report
print('z_stat: %0.3f, p_value: %0.3f' % (stat, p_value))

if p_value > significance:
   print ("Fail to reject the null hypothesis - we have nothing else to say")
else:
   print ("Reject the null hypothesis - suggest the alternative hypothesis is true")

2-sample z-test

Compare the proportions between 2 samples

Here we have two samples, defined by a proportion, and we want to see if we can make an assertion about whether the overall proportions of one of the underlying populations is greater than / less than / different to the other.

In this example, we want to compare two different populations to see how their tests relate to each other:

We have two samples – A and B. Our null hypothesis is that the proportions from the two populations are the same
Our alternative hypothesis is that the proportions from the two populations are different
From one population we sampled 500 tests and found 410 passed
From the other population, we sampled 400 tests and found 379 passed
We use a 2-sample z-test to check if the sample allows us to accept or reject the null hypothesis

To calculate the p-value in Python:

from statsmodels.stats.proportion import proportions_ztest
import numpy as np

# can we assume anything from our sample
significance = 0.025

# our samples - 82% are good in one, and ~79% are good in the other
# note - the samples do not need to be the same size
sample_success_a, sample_size_a = (410, 500)
sample_success_b, sample_size_b = (379, 400)

# check our sample against Ho for Ha != Ho
successes = np.array([sample_success_a, sample_success_b])
samples = np.array([sample_size_, sample_size_b])

# note, no need for a Ho value here - it's derived from the other parameters
stat, p_value = proportions_ztest(count=successes, nobs=samples,  alternative='two-sided')

# report
print('z_stat: %0.3f, p_value: %0.3f' % (stat, p_value))

if p_value > significance:
   print ("Fail to reject the null hypothesis - we have nothing else to say")
else:
   print ("Reject the null hypothesis - suggest the alternative hypothesis is true")

In the next post I will focus on hypothesis testing mean-based samples.

PART I: An Introduction to Hypothesis Testing
PART III: Hypothesis Testing of mean-based samples
PART IV: Hypothesis Testing of frequency-based samples